martes, 18 de marzo de 2014
viernes, 14 de marzo de 2014
lunes, 10 de marzo de 2014
domingo, 9 de marzo de 2014
LA PROPORCIÓN ÁUREA
En realidad se le ha asignado muchas definiciones y nombres; El número de oro, el número dorado o número áureo, número phi, sección áurea, razón áurea, razón dorada, medida áurea o divina proporción. Representado por la letra griega Phi = 1,618034 en honor al escultor griego Fidias. Un número phi(que leemos "Fi") que posee muchas propiedades interesantes y a la vez emocionantes que fue descubierto en la antigüedad, no como una “unidad” sino como una relación o proporción.
Qué es la proporción áurea y su historia
Si recordamos la historia en busca del concepto de divina proporción. Leonardo Pisano, también conocido como Fibonacci, fue un famoso matemático de Italia que se dedicó a divulgar por Europa el sistema de numeración árabe (1, 2, 3…) con base decimal y con un valor nulo (el cero) en su Libro del ábaco en 1202. Pero el gran descubrimiento de este matemático fue la Sucesión de Fibonacci que, posteriormente, dio lugar a la proporción áurea en arte.
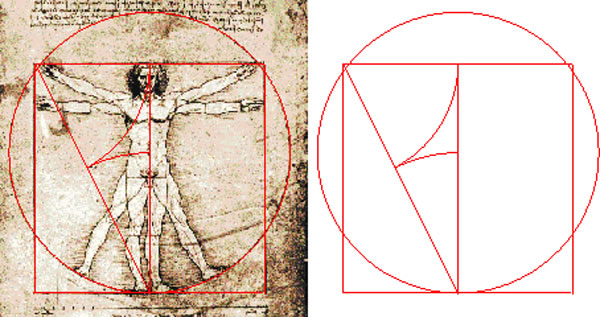Es
durante el Renacimiento, cuando muchísimos artistas y arquitectos
compusieron sus trabajos según la proporción Áurea, convencidos de que
esta relación atribuía a las obras un carácter estético especial. El
hombre de Vitrubio, dibujado por Leonardo Da Vinci y considerado un
ideal de belleza, está proporcionado según el número áureo o incluso la
mismísima Gioconda.¿Qué es la Sucesión de Fibonacci?
Se trata de una serie numérica: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. Es una serie infinita en la que la suma de dos números consecutivos siempre da como resultado el siguiente número (1+1=2; 13+21=34). La relación que existe entre cada pareja de números consecutivos (es decir, si dividimos cada número entre su anterior) se aproxima al número áureo (1,618034). numero phi
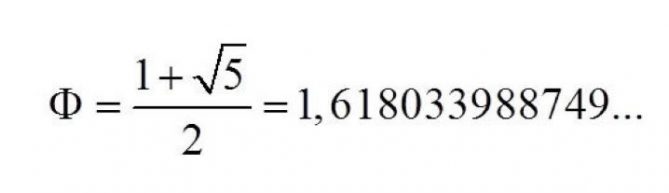
A.- Si trasladamos la secuencia numérica anterior a un rectángulo nos encontramos con el siguiente ejemplo para una mejor comprensión: rectangulo aureo
B.- Si seguimos la división con la sucesión de Fibonacci: numero de oro
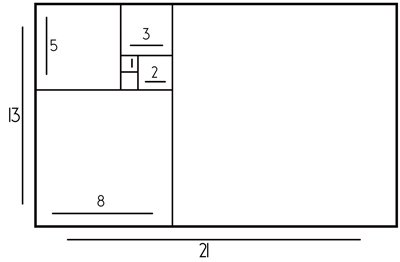
C.- Al unir diferentes vértices con una línea nos aparecerá la famosa Espiral de Oro que se encuentra muy presente en la naturaleza resultando visualmente una proporción “natural”: La divina proporción
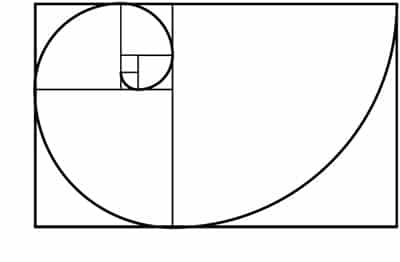
Sección de la caparazón
de un nautilus.
Mueble del diseñador Roberto Cardil.
El famoso arquitecto Frank Lloyd Wright (1867–1959) diseñó la rampa de acceso al museo Guggenheim de Nueva York, con forma de nautilus, o una espiral logarítmica.
Museo Guggenheim, Nueva York
La concha del nautilus es el mejor ejemplo de espiral logarítima encontrada en la naturaleza y que ahora inspira obras arquitectónicas. Las espirales logarítmas aparecen como consecuencia de un movimiento giratorio asociado a un crecimiento tridimensional uniforme en tiempos iguales. La espiral logarítmica fue estudiada por Descartes, y posteriormente, Jakob Bernouilli le dedicó un libro y la llamó Spira mirabilis «la espiral maravillosa».
Herramienta para calcular la proporción aúrea
calculadora
Y podemos ampliar con los siguientes temas
El Modulator de Le Corbusier
La proporción áurea en la arquitectura moderna
La proporción áurea en la ingeniería
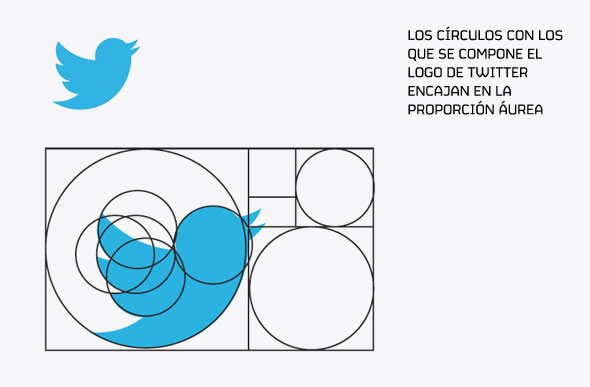
La proporción en el diseño gráfico
Otras aplicaciones de la proporción áurea
Suscribirse a:
Entradas (Atom)